Diposting oleh
kevin wahyu
,
06.44
Rumus Turunan (Diferensial) Matematika
Rumus Turunan (diferensial) Matematika dan Contoh Soal – Dua buah pepatah, kalau tak kenal maka tak sayang dan kalau tahu caranya tidak ada yang tidak bisa mungkin cocok buat jadi pemacu sobat belajar matematika. Jika kita tidak kenal dan tidak tahu cara mengerjakan suatu soal matematika bisa dipastikan soal tersebut tidak bisa kita jawab. Nah kali ini kita akan coba kenalan dengan rumus-rumus di limit matematika SMA. Ada yang bilang limit matematika itu susah. Benar sih susah jika sobat tidak tahu carannya. Berikut ini rangkuman rumus limit beserta contoh soal sederhananya. Check this out?
Apa Sih Turunan?
Definisi turunan aga susah kalau di berikan dalam bentuk kata (verbal). Sobat bisa misalkan ada y yang merupakan fungssi dari x, ditulis y = f(x). Yang dimaksud dengan turun y terhadap x (dinotasikan dy/dx) atau sering ditulis y’ (baca : “y aksen”) didefinisikan sebagai

masih bingung? kita simak contoh berikut
sobat punya persamaan y = 4x maka nilai dari turunan tersebut menurut definisi di atas adalah
Rumus – Rumus Turunan Fungsi Matematika
Buat memudahkan sobat belajar berikut rumushitung.com rangkumkan berbagai rumus turuna. Check this out..

Rumus 1 : Jika y = cxn dengan c dan n konstanta real , maka dy/dx = cn xn-1
contoh
y = 2x4 maka dy/dx = 4.2x4-1 = 8x3
kadang ada soal yang pakai pangkat pecahan atau akar
y = 2√x = 2x1/2 turunannya adalah 1/2.2 x (1/2-1) = x -1/2 = 1/√x
Rumus 2 : Jika y = c dengan c adalah konstanta maka dy/dx = 0
contoh jika y = 6 maka turunannya adalah sama dengan nol (0)
Rumus 3 : Jika y = f(x) + g(x) maka turunannya sama dengan turunan dari masing-masing fungsi = f'(x) + g'(x)
contoh
y = x3 + 2x2 maka y’ = 3x2 + 4x
y = 2x5 + 6 maka y’ = 10x4 + 0 = 10x4
Rumus 4 : Turunan Perkalian Fungsi Jika y f(x).g(x) maka y’ = f'(x) . g(x) + g'(x) . f(x)
contoh
y = x2 (x2+2) maka
f(x) = x2
f'(x) = 2x
g(x) = x2+2
g'(x) = 2x
kita masukkan ke rumus y’ = f'(x) . g(x) + g'(x) . f(x)
y’ = 2x (x2+2) + 2x . x2
y’ = 4x3 + 4x (jawaban ini juga bisa sobat peroleh dengan mengalikan terlebih dahulu lalu menggunakan rumus 3)
Rumus 5 : Turunan Pembagian Fungsi

contoh soalnya
Rumus 6 : jika sobat punya y = [f(x)]n maka turunannya adalah n [f(x)]n-1 . f'(x)
contoh
Diposting oleh
kevin wahyu
,
06.43
Limit Fungsi Aljabar
Matematikastudycenter.com- Contoh soal dan pembahasan limit fungsi aljabar matematika SMA kelas 11.
Dibahas
limit x → a
lim x → ∞ termasuk juga limit x → 0
Mulai dari yang mudah dulu, tipe soal-soal limit yang bisa diselesaikan dengan substitusi langsung seperti contoh berikut.
Soal No. 1Tentukan hasil dari:

PembahasanLimit bentuk

diperoleh

Soal No. 2 Pembahasan
PembahasanLimit aljabar bentuk

Substitusikan saja nilai x,

Berikutnya dilanjutkan dengan tipe metode turunan yaitu limit x menuju angka tertentu dimana jika disubstitusikan langsung mendapatkan hasil yang tak tentu.
Soal No. 3
| Tentukan nilai dari |  |
PembahasanJika angka 2 kita substitusikan ke x, maka akan diperoleh hasil 0/0 (termasuk bentuk tak tentu), sehingga selesaikan dengan metode turunan saja.
 Soal No. 4
Soal No. 4
| Tentukan nilai dari |  |
PembahasanMasih menggunakan turunan
 Soal No. 5
Soal No. 5
| Nilai |  |
A. −1/4
B. −1/2
C. 1
D. 2
E. 4
(Soal Limit Fungsi Aljabar UN 2012)
Pembahasan
Bentuk 0/0 juga, ubah bentuk akarnya ke bentuk pangkat agar lebih mudah diturunkan seperti ini

Turunkan atas - bawah, kemudian masukkan angka 3 nya

Soal No. 6Nilai dari

A. 16
B. 8
C. 4
D. -4
E. -8
(Matematika IPS 013)PembahasanBentuk 0/0 juga, dengan turunan:

atau dengan cara pemfaktoran:
Soal No. 7Nilai

A. − 2/9
B. −1/8
C. −2/3
D. 1
E. 2
un matematika 2007PembahasanDengan substitusi langsung akan diperoleh bentuk 0/0.
Cara Pertama
Perkalian dengan sekawan dan pemfaktoran:


Diposting oleh
kevin wahyu
,
06.41
Dimensi Tiga Jarak Titik Garis Kubus atau Limas
Matematikastudycenter.com- Contoh soal pembahasan dimensi tiga kubus, limas tentang jarak antar titik atau titik ke garis materi kelas 10 SMA.
 Soal No. 1
Soal No. 1Kubus dengan panjang sisi 12 cm.
Tentukan
a) panjang diagonal bidang sisi kubus
b) panjang diagonal ruang
PembahasanAF adalah salah satu contoh diagonal bidang pada kubus, sementara BH adalah salah satu contoh diagonal ruang pada kubus.

Panjang diagonal bidang dan diagonal dari kubus dengan panjang sisi = a masing-masing adalah

Sehingga
a) panjang diagonal bidang = 12√2 cm
b) panjang diagonal ruang = 12√3 cm
Soal No. 2Kubus ABCD.EFGH dengan panjang sisi 12 cm. Titik P adalah perpotongan diagonal bidang ABCD. Tentukan jarak titik P ke titik G
PembahasanGambar sebagai berikut

AC panjangnya 12√2, sementara PC adalah setengah dari AC. Sehingga PC = 6√2 cm. CG = 12 cm.
 Soal No. 3
Soal No. 3Pada kubus ABCD.EFGH dengan panjang rusuk 6 cm, jarak titik B ke diagonal ruang AG adalah...
A. √5
B. 2√5
C. 3√5
D. 2√6
E. 3√6
(UN 2003)
PembahasanMisalkan jaraknya adalah BP, dimana BP dengan AG harus tegak lurus.

Ambil segitiga ABG sebagai acuan perhitungan. Jika AB dijadikan alas segitiga, maka BG menjadi tingginya. Jika AG yang dijadikan alas, maka tinggi segitiganya adalah BP, dimana BP itulah yang hendak dicari.


Diposting oleh
kevin wahyu
,
06.40
Soal Pembahasan Logika Matematika
Matematikastudycenter.com- Contoh soal dan pembahasan logika matematika SMA materi kelas 10 tercakup di dalamnya negasi atau ingkaran suatu pernyataan, penggabungan pernyataan majemuk dengan konjungsi, disjungsi, implikasi, biimplikasi dan penarikan kesimpulan dari beberapa premis dan pernyataan yang setara.
Soal No. 1
Tentukan negasi dari pernyataan-pernyataan berikut:
a) Hari ini Jakarta banjir.
b) Kambing bisa terbang.
c) Didi anak bodoh
d) Siswa-siswi SMANSA memakai baju batik pada hari Rabu.
Pembahasan
a) Tidak benar bahwa hari ini Jakarta banjir.
b) Tidak benar bahwa kambing bisa terbang.
c) Tidak benar bahwa Didi anak bodoh
d) Tidak benar bahwa siswa-siswi SMANSA memakai baju batik pada hari Rabu.
Atau boleh juga dengan format berikut:
a) Hari ini Jakarta tidak banjir.
b) Kambing tidak bisa terbang.
c) Didi bukan anak bodoh
d) Siswa-siswi SMANSA tidak memakai baju batik pada hari Rabu.
Soal No. 2
Tentukan negasi (ingkaran) dari pernyataan-pernyataan berikut:
a) p : Semua dokter memakai baju putih saat bekerja.
b) p : Semua jenis burung bisa terbang
c) p : Semua anak mengikuti ujian fisika hari ini.
Pembahasan
Pernyataan yang memuat kata "Semua" atau "Setiap" negasinya memuat kata "Beberapa" atau "Ada" seperti berikut:
a) ~p : Ada dokter tidak memakai baju putih saat bekerja.
b) ~p : Beberapa jenis burung tidak bisa terbang
c) ~p : Beberapa anak tidak mengikuti ujian fisika hari ini.
Soal No. 3
Ingkaran dari pernyataan “Beberapa bilangan prima adalah bilangan genap” adalah....
A. Semua bilangan prima adalah bilangan genap.
B. Semua bilangan prima bukan bilangan genap.
C. Beberapa bilangan prima bukan bilangan genap.
D. Beberpa bilangan genap bukan bilangan prima.
E. Beberapa bilangan genap adalah bilangan prima.
(Soal UN Matematika Tahun 2008 P12)
Pembahasan
p : Beberapa bilangan prima adalah bilangan genap
~p : Semua bilangan prima bukan bilangan genap
Soal No. 4
Tentukan pernyataan majemuk hasil penggabungan pasangan-pasangan pernyataan berikut dengan menggunakan operasi konjungsi (DAN):
a) p : Hari ini Jakarta hujan
q : Hari ini Jakarta banjir
b) p : Iwan memakai topi
q : Iwan memakai dasi
c) p : Mahesa anak jenius.
q : Mahesa anak pemalas.
Pembahasan
a) p : Hari ini Jakarta hujan
q : Hari ini Jakarta banjir
p ∧ q : Hari ini Jakarta hujan dan banjir
b) p : Iwan memakai topi
q : Iwan memakai dasi
p ∧ q : Iwan memakai topi dan dasi
c) p : Mahesa anak jenius.
q : Mahesa anak pemalas.
p ∧ q : Mahesa anak jenius tetapi pemalas
Kata "dan" bisa diganti dengan "tetapi", "walaupun", "meskipun" selaraskan dengan pernyataan.
Soal No. 5
Diberikan dua pernyataan sebagai berikut:
a) p : Hari ini Jakarta hujan lebat.
q : Hari ini aliran listrik putus.
Nyatakan dengan kata-kata:
a) p ∧ q
b) p ∧ ~q
c) ~p ∧ q
d) ~p ∧ ~q
Pembahasan
a) Hari ini Jakarta hujan lebat dan aliran listrik putus
b) Hari ini Jakarta hujan lebat dan aliran listrik tidak putus
c) Hari ini Jakarta tidak hujan lebat dan aliran listrik putus
d) Hari ini Jakarta tidak hujan lebat dan aliran listrik tidak putus
Soal No. 6
Diberikan data:
Pernyataan p bernilai salah
Pernyataan q bernilai benar
Tentukan nilai kebenaran dari konjungsi di bawah ini:
a) p ∧ q
b) p ∧ ~q
c) ~p ∧ q
d) ~p ∧ ~q

Diposting oleh
kevin wahyu
,
06.37
Sistem Persamaan Linear Kuadrat SPLK 10 SMA
Matematikastudycenter.com- Contoh soal dan pembahasan sistem persamaan linear dan kuadrat materi matematika kelas 10 SMA.
Persamaan linier dua variabel x dan y digabungkan dengan persamaan yang mengandung x2 atau y2 SPLK dan SPLDV.
Soal No. 1
Diberikan dua buah persamaan yaitu persamaan linear dua variable dan kuadrat sebagai berikut:
(i) y = 2x + 3
(ii) y = x2 − 4x + 8
Tentukan himpunan penyelesaian (Hp) dari kedua persamaan tersebut di atas!
PembahasanSubstitusikan y dari persamaan (i) ke y pada persamaan (ii), atau sebaliknya dari (ii) ke (i), lanjutkan dengan operasi aljabar.
x
2 − 4x + 8 = 2x + 3
x
2 − 4x + 8 − 2x − 3 = 0
x
2 − 6x + 5 = 0
Berikutnya faktorkan:
x
2 − 6x + 5 = 0
(x − 1)(x − 5) = 0
Dapatkan nilai x yang pertama:
x − 1 = 0
x = 1
Dapatkan nilai x yang kedua:
x − 5 = 0
x = 5
Berikutnya mencari nilai-nilai dari y dengan substitusi nilai x ke persamaan (i):
Untuk x = 1 maka
y = 2x + 3
y = 2(1) + 3
y = 2 + 3
y = 5
Dari sini didapatkan pasangan (x, y) yaitu (1, 5)
Untuk x = 5 maka
y = 2x + 3
y = 2(5) + 3
y = 10 + 3
y = 13
Dari sini didapatkan pasangan (x, y) yaitu (5, 13)
Sehingga himpunan penyelesaiannya Hp :{(1, 5), (5, 13)}
Jika lupa bagaimana cara memfaktorkan,
bisa dibaca lagi.
Soal No. 2Diberikan dua buah persamaan sebagai berikut:
(i) y = 5x + 4
(ii) y = x
2 + 13x − 16
Pembahasanx
2 + 13x − 16 = 5x + 4
x
2 + 13x − 16 − 5x − 4 = 0
x
2 + 8x − 20 = 0
(x + 10)(x − 2) = 0
Nilai x yang pertama
x + 10 = 0
x = − 10
Nilai x yang kedua
x − 2 = 0
x = 2
Nilai-nilai y, dari persamaan pertama:
Untuk x = − 10 didapat nilai y
y = 5x + 4
y = 5(−10) + 4 = − 46
Untuk x = 2, didapat nilai y
y = 5x + 4
y = 5(2) + 4 = 14
Hp : {(− 10, − 46), (2, 14)}

Diposting oleh
kevin wahyu
,
06.16
A. Nilai Mutlak
Nilai mutlak adalah jarak pada garis bilangan real antara bilangan yang dimaksud dengan dengan nol.
untuk

bilangan real didefinisikan
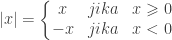
Contoh:

,

,
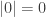
B. Persamaan Nilai Mutlak
Sifat-sifat nilai mutlak
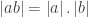

 , (ketaksamaan segitiga)
, (ketaksamaan segitiga)


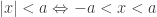
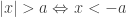 atau
atau 
Contoh Soal:
1. Tentukan nilai

yang memenuhi
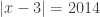
Jawab:
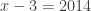 ………………… 1)
………………… 1) ……………. 2)
……………. 2)
Dari persamaan (1) diperoleh

, dan dari persamaan (2) diperoleh
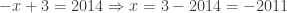
.
Jadi, nilai

yang memenuhi adalah

atau
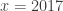
2. Tunjukkan bahwa

Bukti:

3. Tentukan nilai

yang memenuhi

Jawab:

————————————————— ,masing-masing ruas dikuadratkan






4. Gambarkanlah grafik

untuk

bilangan real!
Jawab :
untuk




dan seterusnya
Perhatikanlah ilustrasi berikut ini



















 Soal No. 1
Soal No. 1







