Diposting oleh kevin wahyu , Rabu, 25 Februari 2015 06.16
Persamaan dan Pertidaksamaan Nilai Mutlak
A. Nilai Mutlak
Nilai mutlak adalah jarak pada garis bilangan real antara bilangan yang dimaksud dengan dengan nol.
untuk  bilangan real didefinisikan
bilangan real didefinisikan 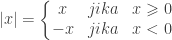
Contoh:
B. Persamaan Nilai Mutlak
Sifat-sifat nilai mutlak
, (ketaksamaan segitiga)
atau
Contoh Soal:
1. Tentukan nilai  yang memenuhi
yang memenuhi 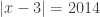
Jawab:
Jawab:
………………… 1)
……………. 2)
Dari persamaan (1) diperoleh  , dan dari persamaan (2) diperoleh
, dan dari persamaan (2) diperoleh 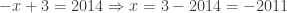 .
.
Jadi, nilai yang memenuhi adalah
yang memenuhi adalah  atau
atau 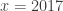
Jadi, nilai
2. Tunjukkan bahwa 
Bukti:
Bukti:
3. Tentukan nilai  yang memenuhi
yang memenuhi 
Jawab:
Jawab:
————————————————— ,masing-masing ruas dikuadratkan
4. Gambarkanlah grafik  untuk
untuk  bilangan real!
bilangan real!
Jawab :
untuk
dan seterusnya
Perhatikanlah ilustrasi berikut ini
Soal Latihan
- Tentukan nilai dari
- Tentukan nilai dari
- Tentukanlah nilai
yang memenuhi persamaan
- Carilah harga
yang memenuhi
- Carilah harga
yang memenuhi
- Tunjukkan bahwa
- Tunjukkan bahwa
- Gambarlah grafik
- Gambarkanlah grafik
, untuk
C. Pertidaksaan Nilai Mutlak
Untuk  bilangan real dan
bilangan real dan  , maka
, maka
- Jika
, maka
Contoh Soal:
1. Tentukanlah himpunan penyelesaian dari 
Jawab:
2. Tentukan penyelesaian dari pertidaksamaan harga mutlak dari 
Jawab :
, atau
Sehingga penyelesaiannya adalah 
3. Tentukan penyelesaian pertidaksamaan harga mutlak dari 
Jawab:
, atau
Jadi, penyelesaiannya adalah 
Sumber:https://ahmadthohir1089.wordpress.com




.jpg)

.jpg)

Posting Komentar